Threat of Adversarial Attacks on Deep Learning in Computer Vision - A Survey

这是一篇神经对抗的综述文章，非常非常非常详细的介绍了当前神经对抗攻击的发展情况和已有的攻击和防御算法。原论文：Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey

Deep learning is at the heart of the current rise of machine learning and artificial intelligence. In the field of Computer Vision, it has become the workhorse for applications ranging from self-driving cars to surveillance and security. Whereas deep neural networks have demonstrated phenomenal success (often beyond human capabilities) in solving complex problems, recent studies show that they are vulnerable to adversarial attacks in the form of subtle perturbations to inputs that lead a model to predict incorrect outputs. For images, such perturbations are often too small to be perceptible, yet they completely fool the deep learning models. Adversarial attacks pose a serious threat to the success of deep learning in practice. This fact has lead to a large influx of contributions in this direction. This article presents the first comprehensive survey on adversarial attacks on deep learning in Computer Vision. We review the works that design adversarial attacks, analyze the existence of such attacks and propose defenses against them. To emphasize that adversarial attacks are possible in practical conditions, we separately review the contributions that evaluate adversarial attacks in the real-world scenarios. Finally, we draw on the literature to provide a broader outlook of the research direction.

本文主要对文章进行翻译，还加入了个人对一些算法的理解与解释。这篇文章我大概看了一个星期。真的是一篇非常不错的综述论文。

---

最近的研究表明，它们很容易受到对抗性攻击，因为输入的细微扰动会导致模型预测不正确的输出。 对于图像来说，这样的扰动往往太小而难以察觉，但它们完全欺骗了深度学习模型

Inroduction

尽管深度学习以非凡的准确性执行各种各样的计算机视觉任务，Szegedy等人[22]首先发现了深度神经网络在图像分类背景下的一个有趣的弱点。他们发现，尽管现代深度网络的准确性很高，但却令人惊讶地容易受到对抗性攻击，这种攻击的形式是对人类视觉系统(几乎)察觉不到的图像的微小干扰。

即使是3d打印现实世界的物体也可以欺骗深度神经网络分类器

在第2节中，我们首先用计算机视觉的说法描述了与对抗性攻击有关的常见术语。在第3节，我们回顾了对抗性攻击任务的图像分类和超越。一个单独的部分是奉献给处理对抗攻击的方法在现实世界的条件。第4节将审查这些方法。在文献中，也有主要分析对抗性攻击存在性的著作。我们将在第5节讨论这些贡献。防御对手攻击的方法是

在adversarial attack中的常用术语

• Adversarial example/image ：被故意扰乱的干净图像的修改版本.
• Threat model ：指一种方法所考虑的潜在攻击类型，例如黑盒攻击.
• Universal perturbation : 可以大概率干扰任何一张图片识别结果的干扰
• White-box attacks ：在知道目标模型的完整知识，包括它的参数值、架构、训练方法，在某些情况下还有它的训练数据的情况下进行攻击.
• Adversarial perturbation ：被加在原图像上的噪声使原图像成为对抗样本
• Adversarial training ：使用对抗图像样本来进行训练
• Adversary ：一般指创造对抗样本的人，有时候样本本身也叫做这个
• Black-box attacks ：测试过程中，在不了解该模型的情况下，为目标模型提供生成的实例的攻击.
• Fooling ratio/rate ：表示经过训练的模型在图像被扰动后改变其预测标签的百分比
• One-shot/one-step methods ：通过执行一步计算产生一个对抗性的扰动，如一次计算模型损失梯度。与之相反的是迭代方法，即多次执行相同的计算以获得单个扰动。
• Quasi-imperceptible ：对于人类的感知来说，干扰对图像的影响非常轻微。
• Rectifier ：修改一个对抗性的示例，以将目标模型的预测恢复为同一示例的干净版本上的预测。
• Targeted attacks ：骗过一个模型，让它错误地预测出敌对形象的特定标签。

3. 神经对抗攻击

第三节中论文主要分为两大部分来进行介绍

在第3.1部分中，我们回顾了攻击深度神经网络的方法，这些方法执行计算机视觉中最常见的任务，即分类/识别。在第3.2部分中讨论了主要用于攻击深度学习的方法。

3.1 Attacks for classification

3.1.1 Box-constrained L-BFGS

Szegedy等人首先证明了图像存在小扰动，如扰动图像可以欺骗深度学习模型，使其误分类。设Ic∈Rm表示一个向量化的干净图像——下标‘c’强调该图像是干净的。为了计算一个可加性扰动ρ∈Rm，它会对图像产生非常轻微的扭曲，从而欺骗网络，Szegedy等人提出解决问题的公式:

$$\min _{\boldsymbol{\rho}}\|\boldsymbol{\rho}\|_{2} \text { s.t. } \mathcal{C}\left(\mathbf{I}_{c}+\boldsymbol{\rho}\right)=\ell ; \mathbf{I}_{c}+\boldsymbol{\rho} \in[0,1]^{m}$$

其中$' \ell^{\prime}$为图像的标签，C(.)为深度神经网络分类器。在这种情况下，上式成为一个困难的问题。因此他们利用box-constrained的L-BFGS寻求一个近似解。这是通过找到最小c > 0来实现的，对于它，下面问题的最小ρ满足条件$\mathcal{C}\left(\mathbf{I}_{c}+\boldsymbol{\rho}\right)=\ell$:

$$\min _{\boldsymbol{\rho}} c|\boldsymbol{\rho}|+\mathcal{L}\left(\mathbf{I}_{c}+\boldsymbol{\rho}, \ell\right) \text { s.t. } \mathbf{I}_{c}+\boldsymbol{\rho} \in[0,1]^{m}$$

$\mathcal{L}(., .)$计算分类器的损失。我们注意到上式使得具有凸损失函数的分类器具有精确的结果。然而，对于深度神经网络来说，情况通常不是这样。计算的扰动只是添加到图像，使它成为一个对抗的例子。

上述方法能够计算当将噪声添加到干净图像时对神经网络的扰动，但是对抗性图像看起来与人类视觉系统的干净图像相似。Szegedy等人观察到一个神经网络计算的扰动也能够欺骗多个网络。这些惊人的结果发现了深度学习中的一个盲点。在这个发现的时候，计算机界正在迅速适应这样一种印象：深度学习特征定义了一个空间，在这个空间中，感知距离可以很好地近似于欧几里德距离。因此，这些相互矛盾的结果引发了研究人员对计算机视觉深度学习对抗性攻击的广泛兴趣。

---

补充说明：L-BFGS算法

参考博客链接：https://blog.csdn.net/weixin_39445556/article/details/84502260

我们知道算法在计算机中运行的时候是需要很大的内存空间的.就像我们解决函数最优化问题常用的梯度下降,它背后的原理就是依据了泰勒一次展开式.泰勒展开式展开的次数越多,结果越精确,没有使用三阶四阶或者更高阶展开式的原因就是目前硬件内存不足以存储计算过程中演变出来更复杂体积更庞大的矩阵.L-BFGS算法翻译过来就是有限内存中进行BFGS算法,L是limited memory的意思.

算法为什么叫做BFGS呢？这就是四个数学家名字的简称而已，不用过多的在意

学习BFGS必须要先了解牛顿法的求根问题.

牛顿法求根问题

牛顿发现,一个函数的根从物理的角度就可以根据函数图像迭代求得.牛顿法求根的思路是:

​ a.在X轴上随机一点x1,经过x1做X轴的垂线,得到垂线与函数图像的交点f（x1）

​ b.通过f（x1）做函数的切线,得到切线与X轴的交点x2

​ c.迭代a/b两步.

​ 下面附上一张动图方便理解:

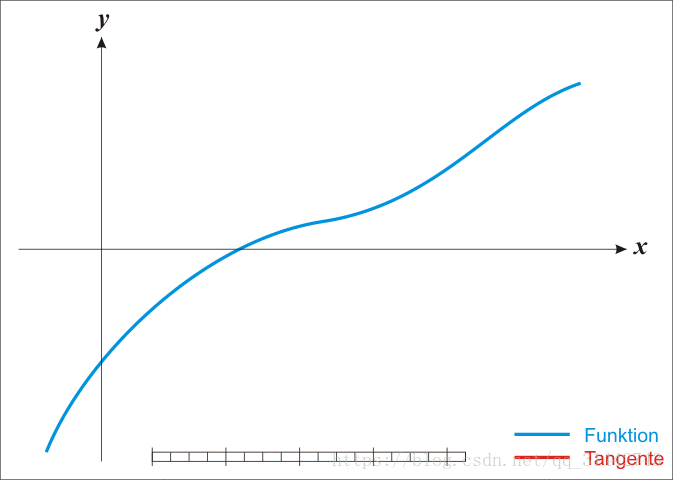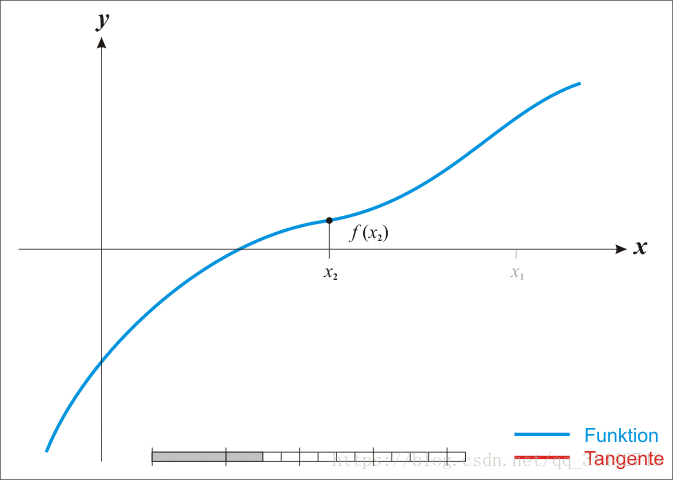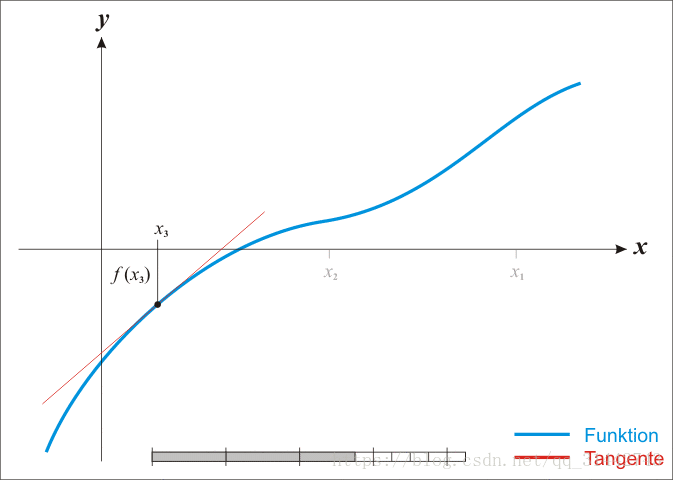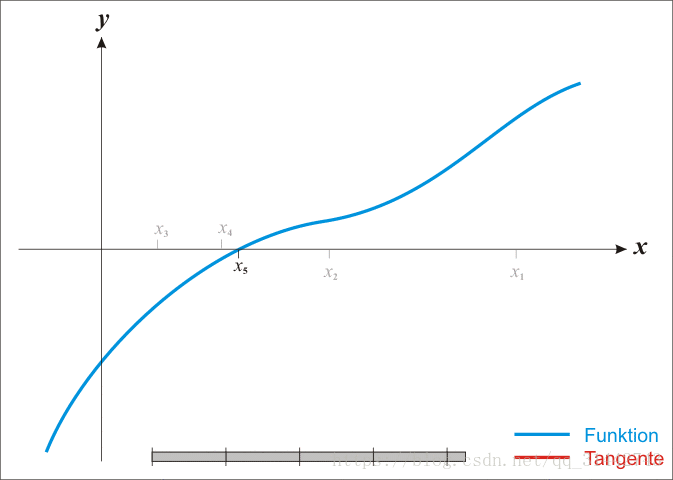
​ 通过图片我们可以看到.在X轴上取的点会随着迭代次数的增加而越来越接近函数的根.经过无限多次的迭代$x_n$,就等于函数f(x)的根.但牛顿法在实际应用的时候我们不会让算法就这么迭代下去,所以当$x_{k-1}$和$x_{k}$相同或者两个值的差小于一个阈值的时候,$x_{k}$就是函数$f(x)$的根.

​ 那么问题来了,怎么样找到$f(x)$的导函数与X轴的交点.请看下图:

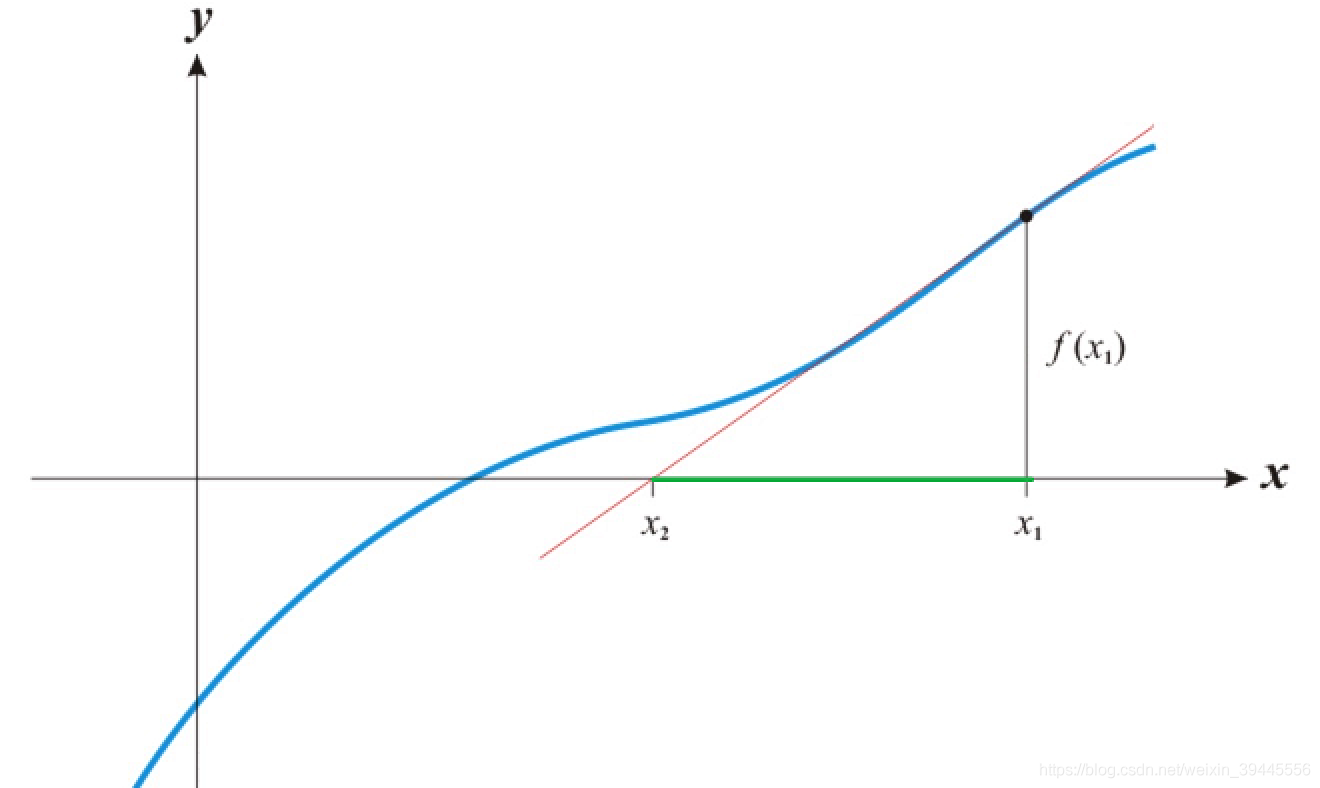
图片是上边动图从$x_{1}$到$x_{2}$的动作.可以看到,三角形绿色的直角边的值是$x_{1} - x_{2}$ , $x_{1}$是已知的(随机出来的),而且函数表达式f(x)也是已知的(不知道要求的函数咱们折腾啥呢).所以三角形的另一条直角边$f(x_{1})$也是已知的.根据导函数定义,函数f(x)在$x_{1}$ 点的导函数就是$f^{'}(x) = \frac{f(x_{1})}{x_{1} - x_{2}}$ (公式一).

公式一变换一下得到: $x_{2} =x_{1} - \frac{ f(x_{1})}{f^{'}(x_{1})}$ (公式二 ),同理可以得出每一次迭代$x_{k}$的表达式都是 $x_{k} =x_{k-1} - \frac{ f(x_{k-1})}{f^{'}(x_{k-1})}$ (公式三).

所以,根据牛顿法求根的思路,我们可以总结(模仿)一下使用牛顿法求根的步骤:

a.已知函数f(x)的情况下,随机产生点$x_{0}$.

b.由已知的$x_{0}$点按照$x_{k} =x_{k-1} - \frac{ f(x_{k-1})}{f^{'}(x_{k-1})}$的公式进行k次迭代.

c.如果$x_{k}$与上一次的迭代结果$x_{k-1}$相同或者相差结果小于一个阈值时,本次结果$x_{k}$就是函数f(x)的根.

以上为牛顿法的求根的思路.

牛顿法求函数的驻点

我们知道,机器学习过程中的函数最优化问题,大部分优化的都是目标函数的导函数,我们要求得导函数为零时的点或近似点来作为机器学习算法表现最好的点.现在我们知道了牛顿求根法,那把牛顿求根法的函数换成咱们要优化的导函数不就行了么.要求的的导函数为零的点叫做驻点.所以用牛顿法求函数驻点同求函数的根是没有任何区别的.只是公式二中的$f(x)$变为了$f^{'}(x)$,原来的$f^{'}(x)$变成了一阶导函数$f^{'}(x)$的导函数也就是二阶导函数$f^{''}(x)$,求$x_{k}$的迭代公式如下:

$x_{k} = x_{k-1} - \frac{f^{'}(x_{k-1})}{f^{''}(x_{k-1})}$ (公式四)

这样,我们通过几何直觉,得到了求解函数根的办法,那这么厉害的一个想法,有没有什么理论依据作为支撑呢?当然有了,要不我也不这么问.

牛顿法求驻点的本质

牛顿法求驻点的本质其实是二阶泰勒展开.我们来看二阶泰勒展开式:

$$\varphi(x)=f\left(x_{k}\right)+f^{\prime}\left(x_{k}\right)\left(x-x_{k}\right)+\frac{1}{2} f^{\prime \prime}\left(x_{k}\right)\left(x-x_{k}\right)^{2}$$

$\varphi (x)$是我们要求解的原函数的近似式.当我们要对原函数求解时,可以直接求得$\varphi (x)$的导函数$\varphi^{'} (x)$ 令$\varphi^{'} (x) = 0$时的结果就是原函数的解.所以对$\varphi (x)$求导,消去常数项后得到公式如下:

$$f^{\prime}\left(x_{k}\right)+f^{\prime \prime}\left(x_{k}\right)\left(x-x_{k}\right)=0$$

经过变换后所得的公式就是上边的公式四.所以,牛顿法求驻点的本质就是对函数进行二阶泰勒展开后变换所得到的结果.

在一元函数求解的问题中,我们可以很愉快的使用牛顿法求驻点,但我们知道,在机器学习的优化问题中,我们要优化的都是多元函数,所以x往往不是一个实数,而是一个向量.所以将牛顿求根法利用到机器学习中时,x是一个向量,$f^{'}(x)$也是一个向量,但是对$f^{'}(x)$求导以后得到的$f^{''}(x)$是一个矩阵,叫做Hessian矩阵.等价公式如下:

$$\mathbf{x}_{k+1}=\mathbf{x}_{k}-H_{k}^{-1} \cdot \mathbf{g}_{k}, \quad k=0,1, \cdots$$

公式中,$g_{k}$为公式四中的$f^{'}(x),H_{k}^{-1}$代表二阶导函数的倒数.

当x的维度特别多的时候,我们想求得$f^{''}(x)$是非常困难的.而牛顿法求驻点又是一个迭代算法,所以这个困难我们还要面临无限多次,导致了牛顿法求驻点在机器学习中无法使用.有没有什么解决办法呢?

BFGS算法

BFGS算法是通过迭代来逼近$H_{k}^{-1}$的算法.逼近的方式如下(公式五):

$$D_{k+1}=\left(I-\frac{\varepsilon_{k} \mathbf{y}_{k}^{T}}{\mathbf{y}_{k}^{T} \mathbf{s}_{k}}\right) D_{k}\left(I-\frac{\mathbf{y}_{\mathbf{s}} \mathbf{s}_{k}^{T}}{\mathbf{y}_{k}^{T} \mathbf{s}_{k}}\right)+\frac{\mathbf{s}_{k} \mathbf{s}^{T}}{\mathbf{y}_{k}^{T} \mathbf{s}_{k}}$$

公式五中的 $D_{k}$就是$H_{k}^{-1}.s_{k} = x_{k+1} - x_{k},y_{k} = g_{k+1} - g_{k}$. $g_{k}$是原函数的导函数.

$D_{k}$的迭代公式复杂无比,还好我们不用记住它.BFGS是通过迭代来逼近$H_{k}^{-1}$矩阵,第一步的D矩阵是单位矩阵.

我们要通过牛顿求驻点法和BFGS算法来求得一个函数的根,两个算法都需要迭代,所以我们干脆让他俩一起迭代就好了.两个算法都是慢慢逼近函数根,所以经过k次迭代以后,所得到的解就是机器学习中目标函数导函数的根.这种两个算法共同迭代的计算方式,我们称之为On The Fly.个人翻译:让子弹飞~

回顾一下梯度下降的表达式$\Theta_{k} = \Theta_{k+1} - \alpha \cdot g$ ,在BFGS算法迭代的第一步,单位矩阵与梯度g相乘,就等于梯度g,形式上同梯度下降的表达式是相同的.所以BFGS算法可以理解为从梯度下降逐步转换为牛顿法求函数解的一个算法.

虽然我们使用了BFGS算法来利用单位矩阵逐步逼近H矩阵,但是每次计算的时候都要存储D矩阵,D矩阵有多大呢.假设我们的数据集有十万个维度(不算特别大),那么每次迭代所要存储D矩阵的结果是74.5GB.我们无法保存如此巨大的矩阵内容,如何解决呢?

使用L-BFGS算法.

L-BFGS算法:

我们每一次对D矩阵的迭代,都是通过迭代计算$s_{k}$和$y_{k}$得到的.既然存不下D矩阵,那么我们存储下所有的$s_{k}$和$y_{k}$想要得到$D_{10}$就用单位矩阵同存储下的$s_{1}$和$y_{1}$到$s_{10}$和$y_{10}$计算就可以了.这样一个时间换空间的办法可以让我们在数据集有10000个维度的情况下,由存储10000 x 10000的矩阵变为了存储十个1 x 10000的10个向量,有效节省了内存空间.

但是,仅仅是这样还是不够的,因为当迭代次数非常大的时候,我们的内存同样存不下.这个时候只能丢掉一些存不下的数据.假设我们设置的存储向量数为100,当s和y迭代超过100时,就会扔掉第一个s和y,存储s{2}到s{101}和y{2}到y{101},每多一次迭代就对应的扔掉最前边的s和y.这样虽然损失了精度,但确可以保证使用有限的内存将函数的解通过BFGS算法求得到.

所以L-BFGS算法可以理解为对BFGS算法的又一次近似.

---

3.1.2 Fast Gradient Sign Method (FGSM)

FGSM是一种白盒攻击；

Szegedy等人[22]观察到，对抗性训练可以提高深层神经网络对对抗性例子的鲁棒性。（对抗性训练就是指将生成的对抗性样本加入到训练集当中来进行进一步的训练）

为了实现有效的对抗性训练，Goodfello等人[23]开发了通过解决以下问题，有效计算给定图像的对抗性扰动的方法：

$$\rho=\epsilon \operatorname{sign}\left(\nabla \mathcal{J}\left(\boldsymbol{\theta}, \mathbf{I}_{c}, \ell\right)\right)$$

$\nabla \mathcal{J}(.,.,.)$计算围绕模型参数当前值的成本函数的梯度;$\epsilon$是限制微扰范数的小标量值。这种方法叫做FGSM（Fast Gradient Sign Method）算法。

有趣的是，FGSM产生的对抗性例子利用了高维空间中深层网络模型的“线性”，而这种模型当时通常被认为是高度非线性的。古德费罗等人[23]假设，现代深层神经网络的设计（有意）为计算增益引入线性行为，也使它们容易受到廉价的分析扰动。在相关文献中，这一观点通常被称为“线性假设”，这一点得到了FGSM方法的证实。

FGSM对图像进行扰动，以增加分类器在结果上的损失。sign函数保证了损失大小最大化，而ε本质上限制了$\ell_{\infty}$ -norm的扰动。Miyato等人[103]提出的计算方法，如下所示：

$$\boldsymbol{\rho}=\epsilon \frac{\nabla \mathcal{J}\left(\boldsymbol{\theta}, \mathbf{I}_{c}, \ell\right)}{\left\|\nabla \mathcal{J}\left(\boldsymbol{\theta}, \mathbf{I}_{c}, \ell\right)\right\|_{2}}$$

在上面的方程中，计算的梯度用$\ell_2$范数正则化。Kurakin等人[80]将该技术称为"快速梯度L2"方法，并提出了使用$\ell_{\infty}$范数进行归一化的替代方法，这个方法被叫做“快速梯度$\ell_{\infty}$”方法。从广义上讲，在计算机视觉对抗性攻击的相关文献中，所有这些方法都被叫做 ‘one-step’ or ‘one-shot’ “一步式”或“一次性”方法。

---

补充说明：FGSM算法

参考文章： 干货 | 攻击AI模型之FGSM算法

FGSM最早由Goodfellow在其论文《Explaining and Harnessing Adversarial Examples》[23] 中提出。以最常见的图像识别为例，我们希望在原始图片上做肉眼难以识别的修改，但是却可以让图像识别模型产生误判。假设图片原始数据为x，图片识别的结果为y，原始图像上细微的变化肉眼难以识别，使用数学公式表示如下。

$$\widetilde{x}=x+\eta$$

将修改后的图像输入分类模型中，x与参数矩阵相乘。

$$w^{T} \widetilde{x}=w^{T} x+w^{T} \eta$$

对分类结果的影响还要受到激活函数的作用，攻击样本的生成过程就是追求以微小的修改，通过激活函数的作用，对分类结果产生最大化的变化。Goodfellow指出，如果我们的变化量与梯度的变化方向完全一致，那么将会对分类结果产生最大化的变化。

$$\eta=\operatorname{\epsilon sign}(\operatorname{grad}(w, x, y))$$

其中sign函数可以保证变化量与梯度函数方向一致。

当x的维数为n时，模型的参数在每个维度的平均值为m，每个维度的微小修改与梯度函数方向一致，累计的效果为：

$$mn \epsilon$$

可见当原始数据的维度越大，攻击的累计效果越明显。以一个更加直观的例子来说明FGSM的原理。

假设具有2000个样本，每个数据具有1000维，每维的数据的数值的大小都在0-1之间随机生成，分类标签只有2种。

import tensorflow as tf
from tensorflow.keras import *
print(tf.__version__)
print(tf.test.is_gpu_available())
import sklearn
from sklearn.preprocessing import MinMaxScaler

# feather number
n_features = 1000
x,y=datasets.make_classification(n_samples=2000,
                                 n_features=n_features,
                                 n_classes=2,
                                 random_state=random_state)
# Standardized to 0-1
x = MinMaxScaler().fit_transform(x)

分类模型是一个非常简单的神经网络，输入层大小为1000，输出层为1，激活函数为sigmoid。

model = tf.keras.models.Sequential([layers.Dense(1,activation='sigmoid')])

sigmoid函数是非常经典的激活函数，取值范围为0-1，特别适合表示概率分布。

损失函数使用最简单的mse，优化方式使用adam，考核的指标为准确度accuracy。

model.compile(loss='mse',optimizer='adam',metrics=['accuracy'])
model.fit(  #使用model.fit()方法来执行训练过程，
    x, y, #告知训练集的输入以及标签，
    batch_size = 16, #每一批batch的大小为32，
    epochs = 50, #迭代次数epochs为500
    validation_split = 0.2, #从测试集中划分80%给训练集
    validation_freq = 10 #测试的间隔次数为20
)

批处理大小为16，经过50轮训练。

model.fit(x_train, y_train, validation_data=(x_val, y_val),
          epochs=100)

最终训练结果，损失值稳定在0.015左右，准确度为70% 左右；

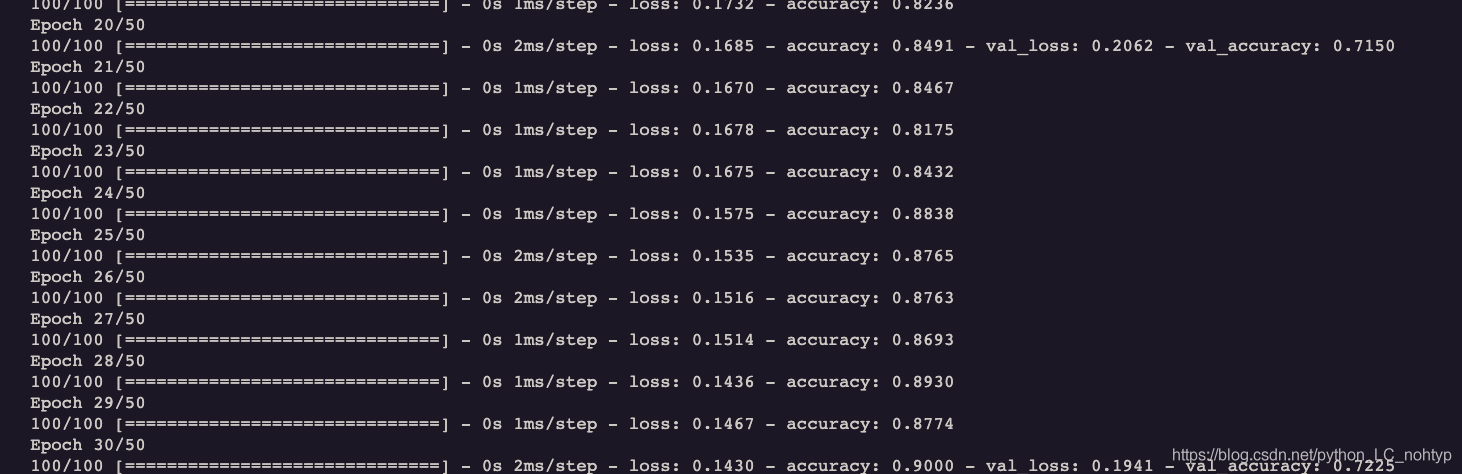
model.summary()

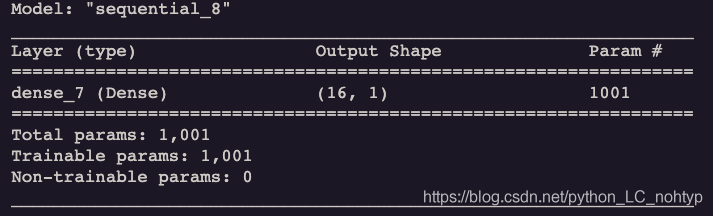
由于数据是随机生成的，我们取1号举例，可以看到标签是0，结果也是很接近1的

import numpy as np
x1 = x[1]
y1 = y[1]
x1 = np.expand_dims(x1,axis=0)
y1_predict = model.predict(x1)
print(y1)
print(y1_predict)

Out:
0
[[0.15540801]]

根据公式：

$$\eta=\operatorname{\epsilon sign}(\operatorname{grad}(w, x, y))$$

我们知道下一步需要计算：模型在x1处的梯度：

x1 = tf.convert_to_tensor(x1)
with tf.GradientTape(persistent=True) as g:
  g.watch(x1)
  y = model(x1)
gradient = g.gradient(y, x1) 

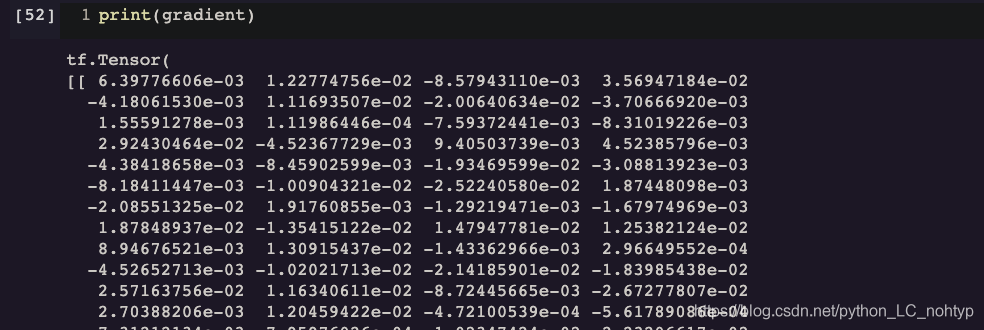
接下来跟着公式进行计算即可：

e我们取0.1 可以认为对原来改变的很小

e = 0.1
n = np.sign(gradient)
x_ = x1 + n * e
print(model(x_))

可以看到预测的结果完全变了！

---

Basic & Least-Likely-Class Iterative Methods

one step方法通过在的方向上迈出一大步（即一步梯度上升）增加分类器的损失来扰动图像。这个想法的一个直观扩展是迭代地采取多个小步骤同时调整每一步后的方向。基本迭代法（BIM）[35]正是这样做的，并且迭代计算如下：

$$\mathbf{I}_{\rho}^{i+1}=\operatorname{Clip}_{\epsilon}\left\{\mathbf{I}_{\rho}^{i}+\alpha \operatorname{sign}\left(\nabla \mathcal{J}\left(\boldsymbol{\theta}, \mathbf{I}_{\rho}^{i}, \ell\right)\right\}\right.$$

$\mathbf{I}_{\rho}^{i}$表示第i次迭代时的扰动图像，Clip 就是剪掉变化过大的部分；

BIM算法从$\mathbf{I}_{\rho}^{0}=\mathbf{I}_{c}$开始，按照公式$\lfloor\min (\epsilon+4,1.25 \epsilon)\rfloor$确定的迭代次数运行。Madry等人[55]指出，BIM等价于投影梯度下降（PGD）的$\ell_{\infty}$版本，PGD是一种标准的凸优化方法。

与将FGSM扩展到 “一步目标类” 变体类似（通过迭代的方式使得图像的识别趋近于某一个类别），Kurakin等人[35]也将BIM扩展到迭代最小可能类方法（ILCM）。在这种情况下，用分类器预测的最不可能类的目标标签$l_{target}$替换中的图像的标签$l$。

ILCM方法生成的对抗性示例已被证明严重影响了分类的精度，即使ε的值非常小，例如<16。

ILCM的实现过程可以说与FGSM如出一辙，区别就在于迭代的次数和诱导分类器预测的目标标签不同；

3.1.4 Jacobian-based Saliency Map Attack (JSMA)

目前通过限制$\ell_{\infty}$ 或者 $\ell_{2}$ -norms来实现对网络扰动的情况比较常见；Papernot等人[60]也通过限制扰动的$l_0$范数来制造对抗性攻击。这意味着目标是只修改图像中的几个像素，而不是干扰整个图像来欺骗分类器。他们生成所需对抗图像的算法关键如下:

• 该算法一次修改一个干净图像的像素，并监控变化对结果分类的影响。
• 通过使用网络层的输出的梯度计算显著性图(computing a saliency map)来执行监视。

在map中，较大的值表示可以成功愚弄网络将$l_{target}$预测为"修改图像"的标签而不是原始标签$l$的可能性较高。一旦map被计算出来，算法就会选择最有效的像素来欺骗网络并改变它。重复这个过程，直到敌对图像中允许的最大像素数被改变，或者愚弄成功。

3.1.5 One Pixel Attack

对抗攻击的一个极端情况是，只改变图像中的一个像素以欺骗分类器。有趣的是，Su等人[68]声称，在70.97%的测试图像上，通过改变每幅图像的一个像素，成功地愚弄了三种不同的网络模型。他们还报告说，网络对错误标签的平均置信度为97.47%。

Su等人利用（Differential Evolution）差异进化的概念计算了对抗性例子[148]。对于一个干净的图像，他们首先在$\mathbb{R}^{5}$中创建了一组400个向量，使得每个向量包含xy坐标；然后给这些向量随机的RGB。

然后，他们随机修改向量的元素来创建子对象，使得子对象在下一次迭代中与其父对象竞争适应度（fitness criterion），同时使用网络的概率预测标签作为适应度准则。最后幸存的子对象用于改变图像中的像素。

即使这样一个简单的进化策略，Su等人[68]也能成功地愚弄了深层网络。注意，差分进化使他们的方法能够产生对抗性的例子，而不需要获得任何关于网络参数值或其梯度的信息。他们的技术需要的唯一输入是目标模型预测的概率标签。让就是说这种攻击的方法属于黑盒攻击；

3.1.6 Carlini and Wagner Attacks (C&W)

卡里尼和瓦格纳[36]提出了一系列的三次对抗性攻击，这是在对抗性干扰[38]的防御升华之后提出的。这些攻击通过限制扰动的$\ell_{2}$、$\ell_{\infty}$和$\ell_{0}$范数使扰动具有准不可察觉性，并且证明了针对目标网络的防御蒸馏几乎完全不能抵抗这些攻击。此外，本文还证明了利用不安全（未蒸馏）网络生成的对抗性例子可以很好地转移到安全（蒸馏）网络，这使得计算出的扰动适合于黑盒攻击。

然而更常见的是利用对抗性例子的可转移性来生成黑盒攻击，Chen等人[41]还提出了基于“零阶优化（ZOO）”的攻击，直接估计目标模型的梯度来生成对抗性例子。这些攻击的灵感来自C&W攻击。

---

补充说明：C&W攻击

3.1.7 DeepFool

Moosavi-dezfouli等人[72]提出了一个迭代计算最小范数对抗性扰动的方法。DeepFool用干净的图像初始化，该图像被假定位于由分类器的决策边界限定的区域中。这个区域决定了图像的类标签。At each iteration, the algorithm perturbs the image by a small vector that is computed to take the resulting image to the boundary of the polyhydron that is obtained by linearizing the boundaries of the region within which the image resides.每次迭代中添加到图像上的扰动被累加，一旦扰动图像根据网络的原始决策界改变其标签，就计算出最终的扰动。作者证明了DeepFool算法能够计算出比FGSM[23]计算的扰动范数更小的扰动，同时具有相似的愚弄率。

实现过程与FGSM也是比较类似的；

下面我们看一下Deep Fool算法和FGSM算法去攻击同一个图像修改量的对比图：

可以看到Deep Fool的修改量明显的要小于FGSM；

除了迭代环节，DeepFool与FGSM的算法完全相同。在迭代环节，我们可以通过NumPy的inalg.norm函数对梯度进行处理，然后迭代更新图片内容。

# Deep Fool 攻击代码的迭代
while cost < 0.6:
  cost,gradients = grab_cost_and_gradients_from_model([hacked_image,0])
  r= gradients*cost/pow(np.linalg.norm(gradients), 2)
  hacked_image +=r
  hacked_image = np.clip(hacked_image, max_change_below, max_change_above)
  hacked_image = np.clip(hacked_image, -1.0, 1.0)
  
# FGSM算法的迭代

while cost < 0.60:
    cost, gradients = grab_cost_and_gradients_from_model([hacked_image, 0])
    n=np.sign(gradients)
    hacked_image +=n*e
    hacked_image = np.clip(hacked_image, max_change_below, max_change_above)
    hacked_image = np.clip(hacked_image, -1.0, 1.0)
  

3.1.8 Universal Adversarial Perturbations

​ 然而像FGSM[23]、ILCM[35]、Deep-Fool[72]等方法计算扰动来愚弄单个图像上的网络，Moosavi Dezfouli等人[16]计算的“普遍”对抗扰动能够以高概率愚弄“任何”网络。如图1所示，这些图像不可知的扰动对于人类视觉系统来说仍然是准不可察觉的。为了正式定义这些扰动，让我们假设干净的图像是从分布$\Im_{c}$采样的。如果扰动ρ满足以下约束条件，则它是“普适的”：

$$\underset{\mathbf{I}_{c} \sim \Im_{c}}{\mathrm{P}}\left(\mathcal{C}\left(\mathbf{I}_{c}\right) \neq \mathcal{C}\left(\mathbf{I}_{c}+\boldsymbol{\rho}\right)\right) \geq \delta \text { s.t. }\|\boldsymbol{\rho}\|_{p} \leq \xi$$

其中$P(.)$表示概率，$\delta \in(0,1]$表示愚弄比率，$\|.\|_{p}$表示$\ell_{p}$范数，$\xi,$是预定义的参数。$\xi,$值越小，就越难察觉图像中的扰动。严格地说，满足上述公式的扰动应称为$(\delta, \xi)$ -universal ，因为它们对上述参数有很强的依赖性。然而，这些扰动在文献中通常被称为普遍的对抗性扰动（universal adversarial pertur- bations）。

作者通过限制 $\ell_{2}$范数和$\ell_{\infty}$范数计算了universal perturbations ，结果表明，对于最先进的图像分类器，其范数上界为各自图像范数的4%的扰动，这样的扰动已经达到了约0.8或着更高的愚弄率。他们计算扰动的迭代方法与DeepFool策略[72]有关，该策略将数据点（即图像）逐渐推到其类的决策边界。然而，在这种情况下，“所有”训练数据点被依次推到各自的决策边界，并且通过每次将累加器向后投影到半径 $\xi$的所需$\ell_{p}$球，在所有图像上计算的扰动被逐渐累积。

Moosavi Dezfouli等人[16]提出的算法在针对单个网络模型时计算扰动，例如ResNet[147]。这些扰动也可以很好地推广到不同的网络（特别是具有相似结构的网络）。从这个意义上说，作者声称扰动在某种程度上是“双重普遍的”。此外，高愚弄率只使用大约2000张训练图像来学习扰动就可以实现了。

Khrulkov等人[190]还提出了一种将普遍对抗性扰动构造为网络特征映射的雅可比矩阵奇异向量的方法，这种方法允许仅使用少量图像获得相对较高的欺骗率。另一种产生普遍扰动的方法是Mopuri等人[135]提出的快速特征愚弄。他们的方法产生了与数据无关的普遍扰动。

3.1.9 UPSET and ANGRI

​ Sarkar等人[146]提出了两种黑盒攻击算法，即 UPSET: Universal Perturbations for Steering to Exact Targets, 和ANGRI: Antagonistic Network for Generating Rogue Images 有针对性地愚弄深层神经网络。对于“n”类，UPSET寻求产生“n”图像不可知扰动，这样当扰动被添加到不属于目标类的图像时，分类器将扰动图像分类为来自该类。UPSET的效果来自一个residual generating network $\mathrm{R}(.),$ 它将目标类“t”作为输入，并生成一个扰动$\mathrm{R}(\mathrm{t})$ 以供愚弄。整体方法使用所谓的UPSET- network解决以下优化问题：

$$\mathbf{I}_{\boldsymbol{\rho}}=\max \left(\min \left(s \mathbf{R}(\mathbf{t})+\mathbf{I}_{c}, 1\right),-1\right)$$

其中，$\mathbf{I}_{c}$中的像素值被标准化在[-1,1]之间，并且$s^{\prime}$是标量. 为确保为有效图像，将剪裁间隔[-1,1]之外的所有值。与图像不可知的UPSET相比，ANGRI以一种密切相关的方式计算图像特定的扰动. ANGRI产生的扰动也被用于有针对性的愚弄。据报道，这两种算法在MNIST[10]和CIFAR-10[152]数据集上都实现了高愚弄率。每一种算法的具体实现我会在接下来的其他文章中逐个进行介绍；

3.1.10 Houdini

​ Cisse等人[131]提出了“Houdini”，这是一种通过生成对抗性的例子来愚弄 "基于梯度学习的算法"。对抗性例子可以根据任务损失进行调整。产生对抗性例子的典型算法采用网络可微损失函数的梯度来计算扰动。然而，任务损失通常不适合这种方法。例如，语音识别的任务损失是基于字错误率的，这不允许直接利用损失函数梯度。Houdini是专门为此类任务生成对抗性示例的。除了可以成功生成攻击分类算法的敌对图像外，Houdini还被证明成功攻击了流行的自动语音识别系统[151]. 作者还通过在黑盒攻击场景中愚弄google voice，证明了语音识别中攻击的可转移性。此外，成功的目标攻击和非目标攻击也证明了深度学习模型的人体姿态估计。

3.1.11 Adversarial Transformation Networks (ATNs)

​ Baluja和Fischer[42]训练了前馈神经网络（feed-forward neural net- works），用于生成对抗其他目标网络或网络集的对抗性示例。训练网络就叫做Adversarial Transformation Networks (ATNs). 通过最小化由两部分组成的联合损失函数，计算了这些网络产生的对抗性例子; 第一部分限制对抗示例与原始图像具有感知相似性，而第二部分旨在改变目标网络对结果图像的预测。

沿着相同的方向，Hayex和Danezis[47]还使用attacker neural network 来学习黑匣子攻击的对抗性例子。在给出的结果中，attacker neural network计算的示例与干净的图像在本质上不可区分，但它们被目标网络以压倒性的概率错误分类-在MNIST数据[10]上将分类精度从99.4%降低到0.77%，在CIFAR-10数据集[152]上将分类精度从91.4%降低到6.8%。

3.1.12 Miscellaneous Attacks

这里论文里列举的实在太多了，就以论文中的表格来概括吧；

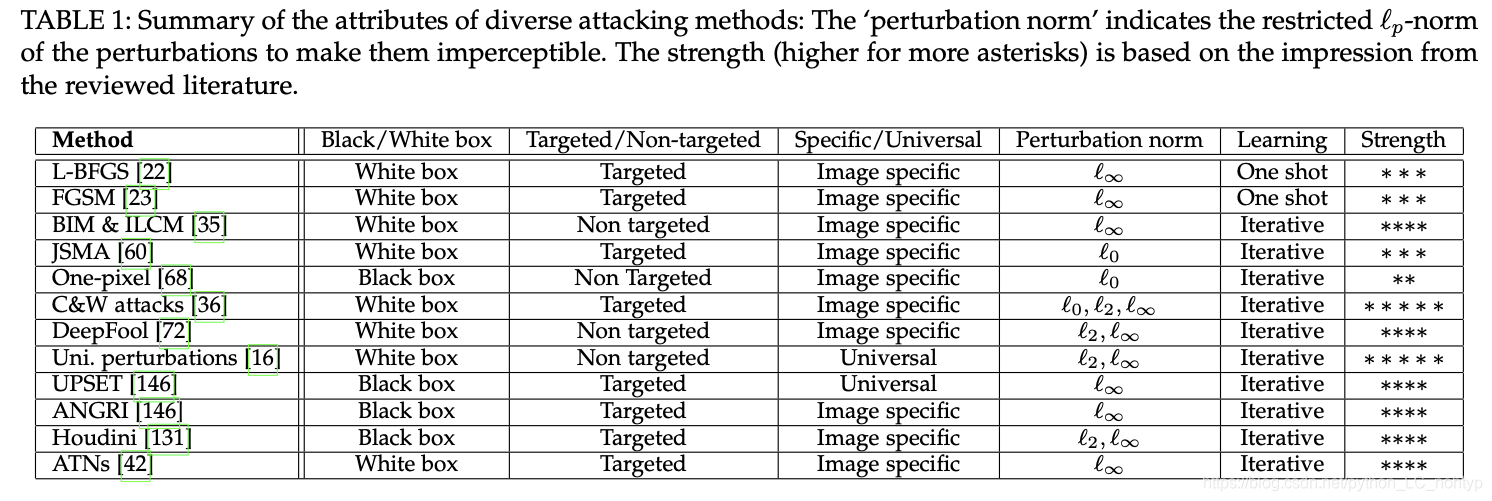
表格中4星以上的攻击方法，之后应该都会出专门的文章进行学习和介绍的，也包括学习过程中的代码实现；

3.2 Attacks beyond classification/recognition

​ 除了Houdini[131]之外，第3.1节中回顾的所有主流攻击都直接集中在分类任务上——通常愚弄基于CNN的分类网络[10]。然而，由于对抗性威胁的严重性，除了计算机视觉中的分类/识别任务外，攻击也被积极地研究。接下来让我们回顾深层神经网络攻击分类之外算法的工作。

3.2.1 Attacks on Autoencoders and Generative Models

Tabacof等人[128]研究了针对autoencoders的对抗性攻击[154]，并提出了一种扭曲输入图像（使其具有对抗性）的技术，这种技术会误导自动编码器重建完全不同的图像。他们的方法攻击神经网络的内部特征，使得攻击图像的特征与目标图像的特征相似。

然而，据[128]报道，与典型的分类器网络相比，自动编码器似乎对对抗性攻击更具鲁棒性。Kos等人[121]还探索了计算深层生成模型的高级示例的方法，例如变分自动编码器（VAE）和VAE生成对抗网络（VAE-GANs）

GAN 像[153]这样的现在在计算机视觉领域非常流行，应用程序可以学习数据分布并生成真实的图像. 作者介绍了针对VAE和VAE-GANs的三种不同类型的攻击。由于这些攻击的成功，我们可以得出结论，深层生成模型也能够攻击,这些攻击会使得输入转化为非常不同的输出。这项工作进一步支持了“ 对抗性例子是当前神经网络结构的普遍现象”这一假设。也就是说当前神经网络普遍会受到对抗性例子的影响；

3.2.2 Attack on Recurrent Neural Networks

​ Papernot等人[110]成功地为递归神经网络（RNN）生成了对抗性输入序列。RNN是一种深度学习模型，特别适合学习顺序输入和输出之间的映射[155]。Papernot等人证明，为前向神经网络（如FGSM[23]）计算对抗性示例的算法也可用于欺骗RNN。特别是，作者成功地愚弄了流行的长短时记忆（LSTM）RNN架构[156]。结论是，循环神经网络模型（如RNN）也不能免疫非循环神经网络（即CNN）中最初发现的对抗性扰动.

3.2.3 Attacks on Deep Reinforcement Learning

Lin等人[134]提出了两种不同的对抗性攻击，专门用于深度强化学习[157]。第一种攻击，被称为“策略定时攻击”，对手通过在一个事件中的一小部分的时间内进行攻击来使得agent的奖励值最小化。这提出了一种确定何时制作和应用对抗性示例的方法，使攻击不被发现。在第二种攻击中，称为‘enchanting attack’（附魔攻击），对手通过集成生成模型和规划算法将agent（智能体）引诱到指定的目标状态。生成模型用于预测agent的未来状态，而规划算法用于生成引诱agent的行为。针对由最先进的深度强化学习算法[157]、[158]训练的代理，成功地测试了这些攻击。

在另一项研究中，Huang等人[62]证明，FGSM[23]也可用于在深度强化学习的背景下显著降低模型的准确度。

3.2.4 Attacks on Semantic Segmentation and Object De- tection

在Moosavi Dezfouli[16]的启发下，Metzen等人[67]证明了图像不可知伦中准不可察觉pertur-bations的存在，这种pertur-bations可以欺骗深层神经网络，显著破坏图像的预测分割。此外，他们还表明，可以计算噪声向量，在保持大部分图像分割不变的情况下（例如，从道路场景中移除行人），从分割的类中移除特定的类。

虽然有人认为“用于语义图像分割的高级扰动空间可能比图像分类的小”，但这种扰动对于不可见的验证图像具有很高的概率去推广。Arnab等人[51]还评估了基于FGSM[23]的用于语义分割的对抗性攻击，并指出许多关于这些用于分类的攻击的观察结果并没有直接转移到分割任务。

Xie等人[115]计算了用于语义分割和目标检测的对抗性示例，观察到这些任务可以表示为对图像中的多个目标进行分类-目标是分割中的一个像素或一个感受野，以及检测中的目标建议。

在这种观点下，他们的方法称为“密集敌方生成”（Dense Adversary Generation），它优化了一组像素/方案上的损失函数，以生成敌方示例。生成的例子被测试来愚弄各种基于深度学习的分割和检测方法。他们的实验评估不仅成功地愚弄了目标网络，而且还表明所产生的扰动在不同的网络模型中具有良好的通用性。在下图中，展示了使用[115]中的方法进行分割和检测的网络欺骗的代表性示例。

4. ATTACKS IN THE REAL WORLD

4.0.1 Attacks on Face Attributes

人脸属性是现代安全系统中新兴的软生物特征识别技术之一。虽然人脸属性识别也可以被归类为一个分类问题，但由于人脸识别本身被视为计算机视觉中的一个主流问题，因此我们分别回顾了这方面的一些有趣的攻击。

Rozsa等人[130]，[160]利用CelebA基准[161]探索了多种深度学习方法的稳定性，通过生成对抗性的例子来改变人脸识别的结果；看下图：

通过使用所谓的“快速翻转属性”技术攻击深度网络分类器，他们发现深度神经网络对对手攻击的鲁棒性在不同的面部属性之间存在很大差异。对抗性攻击可以有效地将目标属性的标签转换为相关属性。

Shen等人[144]提出了两种不同的技术来生成具有高“吸引力分数”但“主观分数”较低的人脸的对抗性示例，用于使用深度神经网络进行人脸吸引力评估。有关人脸识别任务的进一步攻击，请参阅[185]。第3节回顾的文献假设对手直接用图像扰动反馈深层神经网络。此外，还使用标准图像数据库评估了攻击的有效性。尽管这些设置已经证明足以说服许多研究人员，对抗性攻击是实践中深入学习的真正关注点，但我们在文献中也遇到了一些实例（例如[48]，[30]）这种担忧被轻描淡写，对抗性的例子被认为“只是好奇的问题”，几乎没有实际的担忧。因此，本节专门介绍在实际情况下处理对抗性攻击的文献，以帮助解决争论

4.1 Cell-phone camera attack

Kurakin等人[35]首先证明了防御攻击的威胁也存在于物理世界中。为了说明这一点，他们打印了敌对的图像，并用手机摄像头拍下了照片。这些图像被输入到Tensor-Flow相机演示应用程序[181]，该应用程序使用谷歌的Inception模型[145]进行对象分类。结果表明，即使通过相机观察，也有很大一部分图像被错误分类。在图6中，示出了原稿的示例。

以下网址还提供了一段视频[https://youtu.be/zQ uMenoBCk ](https://youtu.be/zQ uMenoBCk )显示了进一步的图像敌对攻击的威胁。这项工作研究了FGSM[23]、BIM和ILCM[35]在物理世界中的攻击方法。

4.2 Road sign attack

​ Etimov等人[75]在[36]和[88]中提出的攻击的基础上，设计了物理世界的鲁棒扰动。他们证明了强大的物理条件，如在视角，距离和分辨率的变化是攻击的可能性。他们提出的算法称为RP2鲁棒物理扰动，用于生成对抗性的例子，道路标志识别系统。这个算法实现了高愚弄率在实际驾车设置。在这项工作中，针对物理路标引入了两种攻击类别：（a）海报打印：攻击者打印一张受到干扰的路标海报，并将其放置在真实的路标上（见下图）（b） 贴纸扰动：印刷在纸上，纸贴在真正的标志上。对于（b）两种类型的扰动进行了研究，（b1）细微扰动：占据整个标志，（b2）伪装扰动：标志上的涂鸦贴纸形式。因此，所有这些干扰都只需要彩色打印机，而不需要其他特殊硬件。成功地产生了（a）和（b）的扰动，使得扰动对物理世界中的自然变化保持鲁棒性，这表明了现实世界中敌对例子的威胁。

​ Lu等人[30]之前曾声称，由于移动车辆中的物理条件不断变化，对抗性示例对于自动车辆中的目标检测不是一个问题。然而，他们所采用的攻击方法[22]、[23]、[35]有些原始。Etimov等人[75]的发现与[66]中的结果正交。然而，在后续研究中，Lu等人[19]表明，像YOLO 9000[149]和FasterrRcnn[150]这样的探测器“目前”没有被Etimov等人[75]引入的攻击所欺骗。在后续研究中，Lu等人[19]表明，像YOLO 9000[149]和Faster rRcnn[150]这样的探测器“目前”没有被Etimov等人[75]引入的攻击所欺骗。Zeng等人[87]还认为，图像空间中的对抗性扰动在物理空间中并不能很好地推广; 然而，Athalye等人[65]表明，我们实际上可以打印3D物体，以便在物理世界中进行成功的对抗性攻击。我们在第4.3节讨论[65]。

​ Gu等人[33]还探讨了一个有趣的概念，神经网络外包训练面临的威胁。他们表明，有可能训练一个在用户的训练和验证样本上表现出最先进性能，但在攻击者选择的输入上表现糟糕的网络（BadNet）。他们在真实场景中演示了这种攻击，创建了一个街道标志分类器，当在停车标志上添加特殊标签时，该分类器将停车标志识别为限速标志。此外，研究发现，即使网络后来用额外的训练数据进行了微调，网络的愚弄行为仍然在合理的程度上存在。

4.3 Generic adversarial 3D objects

Athalye等人[65]介绍了一种构建3D对象的方法，这种方法可以在各种角度和视点上愚弄神经网络。他们的“对变换的期望”（EOT）框架能够构建对整个图像/对象变换分布具有对抗性的示例。他们的端到端方法能够打印任意对抗性的3D对象。在我们看来，这项工作的结果确定，对抗性攻击是一个真正的关注在物理世界的深入学习。图8展示了一个3D打印海龟的例子，它被EOT框架修改为步枪。以下网址提供了演示物理世界中被EOT愚弄的视频：https://www.youtube.com/watch?v=YXy6oX1iNoA&feature=youtu.be

4.4 Cyberspace attacks

Papernot等人[39]在现实世界中对网络空间中的深层神经网络分类器发起了第一次攻击。他们在合成数据上训练了一个替代网络来代替目标黑盒分类器，并举例说明了MetaMind、Amazon和Google对远程托管神经网络的攻击。他们能够证明各自的目标网络错误地分类了84.24%，96.19%和88.94%的由他们的方法产生的对抗性例子。实际上，攻击者在其威胁模型中唯一可用的信息是目标网络的输出标签，用于攻击者提供的输入图像。

在一项相关的工作中，Liu等人[88]开发了一种基于集合的攻击，并展示了它对攻击的成功。

Grosse等人[61]展示了为用作恶意软件分类工具的神经网络构建有效的通用攻击。与图像识别相比，恶意软件分类领域在对抗性设置中引入了额外的约束，如用离散输入代替连续输入域，用要求等价功能行为代替视觉相似性条件。然而，Grosse等人[61]表明，创建有效的对抗性示例对于恶意软件分类仍然是可能的。在[64]、[107]、[125]中还可以找到针对基于深度学习的恶意软件分类的成功对手攻击的更多示例。

5 EXISTENCE OF ADVERSARIAL EXAMPLES

​ 在有关计算机视觉深度学习中的对抗性攻击的文献中，关于对抗性例子存在着不同的观点。这些观点通常与研究人员在攻击或防御深层神经网络时所做的局部经验观察很好地吻合。然而，它们在普及性方面往往不够。例如，Goodfello等人[23]流行的线性假设很好地解释了FGSM和相关攻击。然而，Tanay和Griffin[74]证明了线性分类器的图像类不会受到敌对示例的影响，这与线性假设不一致。更不用说，线性假设本身与先前流行的观点有很大的偏差. 对抗性的例子来源于深度神经网络引起的高度非线性的决策边界。文献中也有其他例子，其中线性假设没有得到直接支持[119]。

​ 决策边界的平坦性[69]、决策边界的大局部曲线[70]和网络的低灵活性[71]是关于存在相互不完全一致的对抗性例子的观点的例子。很明显，只需修改图像中的一个像素就可以形成对抗性示例，但目前的文献似乎对存在对抗性示例的原因缺乏共识。这一事实也使得对抗性例子的分析成为一个积极的研究方向，有望探索和解释由深度神经网络（目前更普遍地被视为黑盒模型）所诱导的决策边界的性质。下面，我们回顾了主要集中在分析对抗性扰动的存在性以进行深入学习的工作。我们注意到，除了下面回顾的文献外，与对抗性攻击（第3节）和防御（第6节）相关的工作通常提供对抗性扰动的简要分析，同时推测导致存在对抗性例子的现象。

5.1 Limits on adversarial robustness

​ Fawzi等人[118]提出了一个研究分类器对 对抗性扰动不稳定性的框架。他们根据数据集类别之间的“可分辨性度量”建立了分类器鲁棒性的基本限制，其中可分辨性定义为线性分类器的两个类别平均值之间的距离和所研究非线性模型的二阶矩矩阵之间的距离分类器。这项工作表明，对抗性的例子也存在于深层神经网络以外的分类中。本文的分析将对抗性不稳定性的现象追溯到分类器的低灵活性，这与当时的主流观点不完全正交，即网络的高非线性使它们容易受到对抗性例子的影响。

5.2 Space of adversarial examples

​ Tabacof和Eduardo[25]在MNIST[10]和ImageNet[11]数据集上生成了浅层和深层网络分类器的对抗性示例，并利用不同分布和强度的噪声探测对抗性示例的像素空间。作者经验性地证明了对抗性例子出现在像素空间的大区域中，这与[23]中的类似主张是一致的。然而，在某种程度上与线性假设相反，他们认为一个弱的、浅的和更线性的分类器也像一个强的深分类器一样容易受到敌对例子的影响。

​ Tramer等人[132]提出了一种估计对抗性例子空间维数的方法。据称，对抗性的例子跨越一个相邻的高维空间（例如，维度≈25）。由于高维性，不同分类器的子空间可以相交，从而导致对抗性例子的可转移性。有趣的是，他们的分析表明，即使分类器容易受到直接攻击，也有可能防御基于传输的攻击。

5.3 Boundary tilting perspective

​ Tanay和Griffin[74]对深层神经网络中存在的对抗性例子提出了“边界倾斜”的观点。他们认为，为了学习和评估分类器而采样的单个类数据通常存在于该类的子流形中，并且当分类边界接近该子流形时，该类存在对抗性示例。他们将分类器的“对抗强度”概念形式化，并将其简化为所考虑的分类器边界和最近的质心分类器之间的“偏离角”。然后证明了分类器的对抗强度可以通过“边界倾斜”决策来改变。作者还认为分类器的对抗稳定性与其正则化有关。在Tanay和Griffin看来，关于存在对抗性例子的线性假设[23]是“不可信的”。

5.4 training cause adversaries预测的不确定性与进化停滞

​ Cubuk等人[91]认为，“对抗性测试的起源主要是由于神经网络对其预测的固有不确定性”。他们根据经验计算了不确定性的函数形式，这与网络结构、训练协议和数据集无关。有人认为，这种形式只依赖于统计的网络逻辑差异。这最终会导致敌对攻击导致的欺骗比率，从而显示出相对于扰动大小的通用缩放。他们研究了基于FGSM[23]、ILCM和BIM[35]的攻击来证实他们的说法。它还声称，网络在清晰图像上的准确性与其对抗性的健壮性相关（关于这个方向的更多论据，见第5.5节）。

​ Rozsa等人[102]假设对抗性干扰的存在是训练图像上决策边界进化停滞的结果。他们认为，一旦分类正确，单个训练样本就不会导致模型（即神经网络）的训练损失，这最终会使它们接近决策边界。因此，通过添加微小的扰动，就有可能将这些（和类似的）样本丢弃到错误的类区域。他们提出了一种批量调整网络梯度（BANG）算法来训练网络，以缓解训练过程中的进化停滞。

5.5 Accuracy-adversarial robustness correlation

​ 为了解释对抗性攻击的存在，Rozsa等人[97]实证分析了八个深度网络分类器的准确度与其对[23]、[94]中介绍的三种对抗性攻击的鲁棒性之间的关系。所研究的分类器包括AlexNet[9]、VGG-16和VGG-19网络[163]、伯克利训练的GoogLeNet和普林斯顿GoogLeNet版本[18]、ResNet-52、ResNet-101和ResNet-152[147]。使用[23]和[94]中提出的技术，借助大型ImageNet数据集[11]生成对抗性示例。他们的实验结果表明，分类精度较高的网络通常对敌方实例也表现出较强的鲁棒性。他们还得出结论，对抗性的例子在相似的网络拓扑之间传输得更好。

5.6 More on linearity as the source

​ Kortov和Hopfield[127]在稠密联想记忆（DAM）模型的背景下检验了普遍扰动的存在[164]。与典型的现代深层神经网络相比，DAM模型采用了神经元之间更高阶（多于二次）的相互作用。作者已经证明，使用具有较小交互功率的DAM模型生成的对抗性测试无法愚弄具有高阶交互的模型，这类似于使用具有ReLU激活的深层神经网络来诱导线性[165]。作者提供了独立于FGSM[23]攻击的对抗性例子存在的经验证据，但支持Goodfello等人[23]的线性假设。

5.7 Existence of universal perturbations

​ Moosavi-Dezfouli等人[16]最初认为，普遍对抗性扰动利用了分类器诱导的决策边界之间的几何相关性。它们的存在部分归功于包含决策边界的nor-mals的子空间，使得法线也围绕着自然图像。在[70]中，他们进一步建立了他们的理论，并证明了存在共同的方向（在数据点之间共享），沿着这些方向，分类器的决策边界可以高度正弯曲。他们认为这样的方向在宇宙扰动的存在中起着关键作用。基于他们的发现，作者还提出了一种新的几何方法来有效地计算普遍对抗摄动。

值得注意的是，先前Fawzi等人[69]也将分类器鲁棒性的理论界与决策边界的曲率联系起来。同样，Tramer等人[77]也认为，数据点附近决策边界的曲率是神经网络易受黑盒攻击的原因。在最近的另一项工作中，Mopuri等人[193]提出了一个类GAN模型来研究给定目标模型的普遍对抗扰动的分布。学习的分布也显示出良好的跨模型传递性。

6 DEFENSES AGAINST ADVERSARIAL ATTACKS

目前，对抗性攻击的防御主要沿着三个方向发展：

1） 在学习过程中使用修改过的训练方式或在测试过程中使用修改过的输入。

2） 修改网络，例如通过添加更多层/子网络、更改丢失/激活功能等。

3） 当分类筛选看不见的示例时，使用外部模型作为网络附加组件。

​ 第一个方法不直接处理学习模型。其他两类更关注神经网络本身。这两类技术又可分为两类，即完全防御和仅检测。“完全防御”方法旨在使目标网络能够在对抗性示例上实现其原始目标，例如，分类器以可接受的精度预测对抗性示例进行预测。另一方面，“仅检测”方法意味着对潜在的对抗性示例发出危险信号，以便在任何进一步处理中拒绝它们。所描述的类别的分类也示于下图中。剩下的部分是根据这个分类法组织的。在所使用的分类法中，“修改”网络和使用“附加组件”的区别在于前者在训练期间对原始的深层神经网络结构/参数进行了更改。另一方面，后者保持原始模型的完整性，并在测试过程中附加外部模型；

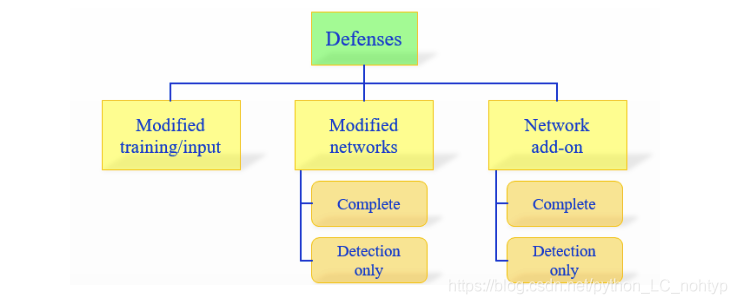
6.1 Modified training/input

6.1.1 Brute-force adversarial training【”蛮力对抗训练“】

​ 自从发现深层神经网络的对抗性例子[22]以来，相关文献中有一个普遍的共识，即神经网络对这些例子的鲁棒性随着对抗性训练而提高。因此，引入新的对抗性攻击的大多数贡献，例如[22]、[23]、[72]（见第3节）同时提出了对抗性训练作为抵御这些攻击的第一道防线。尽管对抗性训练提高了网络的健壮性，但要想真正有效，它需要使用强攻击进行训练，并且网络的体系结构具有足够的表现力。由于对抗性训练需要增加训练/数据量，我们称之为“暴力的“策略。

​ 文献中还普遍观察到，暴力对抗训练可使网络正规化（例如，见[23]，[90]），以减少过拟合，进而提高网络抵抗对抗攻击的鲁棒性。受此启发，Miyato等人[113]提出了一种“虚拟对抗训练”方法来平滑神经网络的输出分布。Zheng等人[116]还提出了一种相关的“稳定性训练”方法，以提高神经网络对输入图像小失真的鲁棒性。值得注意的是，尽管对抗性训练可以提高神经网络的鲁棒性，但Moosavi Dezfouli[16]表明，对于已经经过对抗性训练的网络，可以再次计算有效的对抗性例子。从这里就可以看出暴力对抗并不是一种很好的方法；

6.1.2 Data compression as defense 【数据压缩防御】

​ Dziugaite等人[123]指出，大多数流行的图像分类数据集都包含JPG图像。基于这一观察，他们研究了JPG压缩对FGSM计算的扰动的影响[23]。据报道，JPG压缩实际上可以在很大程度上扭转FGSM扰动导致的分类精度下降。然而，我们得出结论，单靠压缩是远远不能有效防御的。Guo等人也对JPEG压缩进行了研究。郭等人[82]也对JPEG压缩进行了研究，以降低对抗性图像的有效性。Das等人[37]也采取了类似的方法，使用JPEG压缩来去除图像中的高频成分，并提出了一种基于集合的技术来对抗FGSM[23]和DeepFool方法[72]产生的敌对攻击。尽管[37]中报告了令人鼓舞的结果，但没有对更强的攻击进行分析。e.g. C&W攻击[36]。此外，Shin和Song[186]已经证明了存在能够在JPEG压缩中幸存的对抗性示例。在我们之前的工作[81]中，我们还发现离散余弦变换（DCT）下的压缩不足以抵御普遍扰动[16]。基于压缩的防御的一个主要限制是，较大的压缩也会导致对干净图像的分类精度损失，而较小的压缩通常不能充分消除对抗性扰动。

​ 在另一个相关的方法中，Bhagoji等人[169]提出使用主成分分析来压缩输入数据，以增强对抗性。然而，Xu等人[140]指出，这种压缩也会破坏图像的空间结构，因此通常会对分类性能产生不利影响。

6.1.3 Foveation based defense 【中心凹防御】

​ Luo等人[119]证明，使用L-BFGS[22]和FGSM[23]的对抗性攻击具有显著的鲁棒性，通过在图像的不同区域应用神经网络的“中心凹”机制是可能的。假设基于CNN的分类器在大型数据集（如ImageNet[11]）上训练，通常对图像中对象的缩放和平移变化具有鲁棒性。然而，这种不变性并没有扩展到图像中的对抗模式。这使得中央凹成为一个可行的选择，以减少在[22]，[23]中提出的对抗性攻击的有效性。然而，中心凹还没有证明其有效性更强大的攻击。

6.1.4 Data randomization and other methods 【数据随机化和其他方法】

​ Xie等人[115]表明，随机调整敌对例子的大小会降低其有效性。此外，在这些示例中添加随机填充也可以降低网络的欺骗率。Wang等人[138]用一个单独的数据转换模块转换输入数据，以消除图像中可能的敌对干扰。在文献中，我们还发现有证据表明，训练期间的数据增强（例如，高斯数据增强[46]）也有助于提高神经网络对敌对攻击的鲁棒性，尽管这一点很小。

6.2 Modifying the network

​ 对于修改神经网络以抵御对手攻击的方法，我们首先讨论了“完全防御”方法。“仅检测”方法在第6.2.8节中单独进行了审查。

6.2.1 Deep Contractive Networks【深度收缩网络】

​ 在使深度学习对对抗性攻击具有鲁棒性的早期尝试中，Gu和Rigazio[24]引入了深度收缩网络（DCN）。结果表明，去噪自动编码器[154]可以减少对抗性噪声，但是将其与原始网络叠加可以使生成的网络更容易受到干扰。基于这一观察，DCNs的训练过程使用了类似于压缩自动编码器的平滑度惩罚[173]。自从DCNs最初被提出以来，已经引入了许多更强的攻击。使用自动编码器实现神经网络对抗鲁棒性的相关概念也可以在[141]中找到。

6.2.2 Gradient regularization/masking 【梯度正则化/掩蔽】

​ Ross和Doshi Velez[52]研究了输入梯度正则化[167]作为对抗鲁棒性的一种方法。他们的方法训练可微模型（例如深层神经网络），同时根据输入的变化惩罚导致输出的变化程度。这意味着，一个小的对抗性扰动不太可能彻底改变训练模型的输出。结果表明，该方法与暴力对抗训练相结合，对FGSM[23]和JSMA[60]等攻击具有很好的鲁棒性。然而，这些方法中的每一种都几乎使网络的训练复杂度增加了一倍，这在许多情况下都是不可行的。

​ 此前，Lyu等人[28]还使用了将网络模型的损失函数梯度与输入相关的概念，以结合网络对基于L-BFGS[22]和FGSM[23]的攻击的鲁棒性。类似地，Shaham等人[27]试图通过在每次参数更新时最小化模型在对抗性示例中的损失来提高神经网络的局部稳定性。他们用最坏情况下的对抗性例子而不是原始数据来最小化模型的损失。在一项相关的工作中，Nguyen和Sinha[44]通过在网络的logit输出中添加噪声，引入了一种基于掩蔽的防御C&W攻击的方法[36]。

6.2.3 Defensive distillation 【防御蒸馏】

​ Papernot等人[38]利用了“蒸馏”的概念[166]，使得深层神经网络能够抵御对手的攻击。Hinton等人[166]引入蒸馏作为一种训练过程，将更复杂网络的知识转移到更小的网络中。Papernot等人[38]引入的程序变体本质上是利用网络的知识来提高自身的健壮性。以训练数据的类概率向量的形式提取知识，并反馈训练原始模型。结果表明，这样做可以提高网络对图像小扰动的恢复能力。[108]中也提供了这方面的进一步经验证据。此外，在后续工作中，Papernot等人[84]还通过解决[38]中遇到的数值不稳定性，扩展了防御蒸馏方法。值得注意的是，第3.1节中介绍的“卡里尼和瓦格纳”（C&W）攻击[36]被认为是成功对抗防御蒸馏技术的。我们还注意到，防御蒸馏也可以看作是“梯度掩蔽”技术的一个例子。然而，鉴于其在文献中的流行性，我们将其单独描述。

6.2.4 Biologically inspired protection

​ Nayebi和Ganguli[124]证明了神经网络对具有高度非线性激活的对抗性攻击的自然鲁棒性（类似于非线性树突计算）。Nayebi和Ganguli[124]证明了神经网络对具有高度非线性激活的对抗性攻击具有自然鲁棒性（类似于非线性树突计算）

​ Krotov和Hopfield[127]的记忆模型也采用了类似的原理来抵抗对抗性例子。考虑到Goodfel-low等人[23]、[124]和[127]的线性假设，现代神经网络对对抗性例子的敏感性似乎是激活线性效应的概念得到了进一步的发展。我们注意到，Brendel和Bethge[187]声称，由于计算的数值限制，这些攻击在生物启发保护（Biologically inspired protection）[124]上攻击失败。稳定计算（Stabilizing the computations）再次成功攻击受保护的网络。

6.2.5 Parseval Networks

​ 西塞等人[131]提出了“Parseval”网络作为对抗性攻击的防御。这些网络通过控制网络的全局Lipschitz常数采用分层正则化。考虑到一个网络可以被看作是一个函数的组合（在每一层），通过为这些函数保持一个小的Lipschitz常数，可以对小的输入扰动进行鲁棒性处理。Cisse等人提出通过用“parseval紧框架”参数化网络的权重矩阵来控制其谱范数[172]，因此命名为“parseval”网络。

6.2.6 DeepCloak

Gao等人[139]建议在处理分类的层之前插入一个掩蔽层。添加的层通过向前传递干净的和敌对的一对图像进行显式训练，并对这些图像对的前一层的输出特征之间的差异进行编码。有人认为，添加层中最主要的权重对应于网络中最敏感的特征（就对抗性操纵而言）。因此，在分类时，这些特征通过强制将添加层的主要权重设为零来掩盖。

6.2.7 Miscellaneous approaches

Zantedeschi等人[46]提出使用有界ReLU[174]来降低图像中敌对模式的有效性，这是使神经网络对敌对攻击具有鲁棒性的其他显著努力之一。Jin等人[120]介绍了一种前馈CNN，它使用加性噪声来减轻对抗性例子的影响。Sun等人[56]提出了“超网络”，它使用统计滤波作为一种方法，使网络健壮。Madry等人[55]从稳健优化的角度研究了对抗性防御。他们表明，与PGD对手进行对抗性训练可以成功地防御一系列其他对手。后来，卡里尼等人[59]也证实了这一观察结果。Na等人[85]采用了一种网络，该网络通过统一的嵌入进行正则化，用于分类和低水平的相似性学习。利用干净嵌入和相应的敌对嵌入之间的距离对网络进行惩罚。斯特劳斯等人[89]研究了一系列方法来保护网络免受干扰。Kadran等人[136]修改了神经网络的输出层，以增强对抗性攻击的鲁棒性。

Wang等人[129]，[122]通过利用网络中的不可逆数据转换开发了可以抵抗神经对抗样本的神经网络。Lee等人[106]开发了多种规则化网络，使用训练目标最小化干净图像和敌对图像的多层嵌入结果之间的差异。Kotler和Wong[96]提出学习基于ReLU的分类器，该分类器对小的对抗性扰动具有鲁棒性。他们训练的神经网络达到高精度（> 90%）对抗规范环境中的任何对抗样本（$\epsilon=0.1$ for $\ell_{\infty}$，在MNIST数据集当中）。Raghunathan等人[189]研究了具有一个隐藏层的神经网络的防御问题。他们的方法在MNIST数据集上生成了一个网络和一个证书，使得对图像像素的干扰不超过ε=0.1的攻击都不会导致超过35%的测试错误。Kolter和Wong[96]以及Raghunathan等人[189]是为数不多的防御敌对攻击的可证明方法。考虑到这些方法在计算上不适用于更大的网络，唯一被广泛评估的防御措施是Madry等人[55]的防御措施，在MNIST上对大epsilon（0.3/1）的准确率为89%，在CIFAR上对中等epsilon（8/255）的准确率为45%。另一个可以被视为具有保证的对抗性攻击/防御的工作线索与深度神经网络的验证有关，例如[191]，[192]。OrOrbia等人[194]的研究表明，对抗性训练的许多不同建议是更普遍的正规化目标实例，他们称之为DataGrad。提出的DataGrad框架可以看作是分层压缩自编码惩罚的扩展。

6.2.8 Detection Only approaches

SafetyNet: Lu等人[66]假设，对抗性的例子在网络（后期）中产生的ReLU激活模式与干净图像产生的模式不同。基于这一假设，他们提出在目标模型上附加一个径向基函数SVM分类器，使得SVM使用由网络后期ReLUs计算的离散码。为了检测测试图像中的扰动，使用支持向量机将其编码与训练样本的编码进行比较。由[23]、[35]、[72]生成的对抗性示例的有效检测通过其框架SafetyNet进行了证明。

Detector subnetwork: Metzen等人[78]提出用一个子网来增强目标网络，该子网被训练用于检测输入中的敌对扰动的二进制分类任务。研究表明，将这样的网络附加到模型的内部层并使用对抗性训练有助于检测使用FGSM[23]、BIM[35]和DeepFool[72]方法产生的扰动。然而，Lu等人[66]后来表明，这种方法同样容易受到反措施的影响。

Exploiting convolution filter statistics: Li和Li[105]利用基于CNN的神经网络中卷积滤波器的统计特性将输入图像分类为干净的或敌对的。利用这些统计量设计了一个级联分类器，并对文献[22]、[114]中方法生成的85%以上的对抗性图像进行了检测。

Additional class augmentation: Grosse等人[57]提出用一个额外的类来增强潜在的目标神经网络模型，在这个类中，模型被训练来分类所有的对抗性例子。Hosseini等人[32]也采用了类似的策略来检测黑匣子攻击。

6.3 Network add-ons

6.3.1 Defense against universal perturbations

Akhtar等人[81]提出了一个防御框架，以抵抗使用普遍扰动产生的对抗性攻击[16]。该框架将额外的“预输入”层附加到目标网络中，并训练它们校正每一个turbed图像，以便分类器的预测与对同一图像的干净版本的预测相同。预输入层称为扰动校正网络（PRN），在不更新目标网络参数的情况下对其进行训练。通过从训练图像的PRN输入-输出差异中提取特征来训练单独的检测器。测试图像首先通过PRN，然后利用其特征检测扰动。如果检测到对抗性干扰，则使用PRN的输出对测试图像进行分类。图10示出了由PRN执行的校正。对去除的模式分别进行检测分析。

6.3.2 GAN-based defense

​ Lee等人[101]使用流行的生成性对抗网络框架[153]来训练对FGSM[23]类攻击具有鲁棒性的网络。作者建议直接沿着generator network训练网络，试图为该网络产生扰动。在训练过程中，分类器不断尝试正确分类干净的和受干扰的图像。我们将此技术归类为“附加”方法，因为作者建议始终以这种方式训练任何网络。在另一个基于GAN的防御中，Shen等人[58]使用网络的生成器部分来校正扰动图像。

6.3.3 Detection Only approaches

Feature squeezing: Xu等人[43]提出利用特征压缩来检测图像的对抗性扰动。他们将两个外部模型添加到分类器网络中，这样这些模型可以减少图像中每个像素的颜色位深度，并对图像进行空间平滑。比较了目标网络对原始图像和压缩图像的预测。如果预测结果之间存在较大差异，则该图像被认为是一个对抗性的例子。尽管[43]证明了这种方法对更经典的攻击的有效性[23]，但后续工作[140]也声称该方法对更强大的C&W攻击的效果相当好[36]。他等人[76]还将特征压缩与[175]中提出的系综方法相结合，以表明防御的强度并不总是通过组合它们而增加。

MagNet: Meng和Chen[45]提出了一个框架，该框架使用一个或多个外部探测器将输入图像分类为敌对或干净。在训练过程中，该框架旨在学习多种清晰图像。在测试阶段，发现远离流形的图像被视为对抗性的，并被拒绝。靠近流形（但不完全在流形上）的图像总是被重组为位于流形上，并且分类器被送入重组后的图像。将附近的图像吸引到干净图像的流形中，并将远处的图像丢弃的概念也启发了框架的名称，即磁铁。值得注意的是，卡里尼和瓦格纳（Carlini and Wagner）[188]最近证明，这种防御技术也可以在稍大的扰动下被击败。

其他方法：Liang等人[50]将图像的扰动视为噪声，并使用标量量化和空间平滑滤波器分别检测这些扰动。在一个相关的方法中，Feinman等人[86]提出通过利用不确定性估计（of dropout neural networks）和在神经网络的特征空间中执行密度估计来检测对抗性扰动。最后，利用所提出的特征，将单独的二值分类器训练成多示例检测器。Gebhart和Schrater[92]将神经网络计算视为图中的信息流，提出了一种通过对诱导图应用持久同调来检测对抗性扰动的方法。

7 OUTLOOK OF THE RESEARCH DIRECTION

​ 在前面的几节中，我们全面回顾了最近关于对抗性攻击深度学习的文献。尽管在技术细节的这些部分中报告了一些有趣的事实，但下面我们将对这一新兴研究方向进行更一般性的观察。在没有深入了解这一领域的技术知识的情况下，讨论为读者提供了更广阔的前景。我们的论点是基于上述文献。

这种威胁是真实存在的：虽然很少有研究表明，对抗性攻击深度学习可能不是一个严重的问题，但大量相关文献表明并非如此。在第3节和第4节中回顾的文献清楚地表明，对抗性攻击可以严重降低深度学习技术在多个计算机视觉任务上的性能。特别是，第4节回顾的文献确定，在现实世界中，深度学习容易受到对抗性攻击。因此，我们可以得出结论，对抗性攻击对实践中的深度学习构成了真正的威胁。

对抗性脆弱性是一种普遍现象：文献回顾表明，在计算机视觉中，不同类型的深层神经网络（如MLPs、CNNs、RNNs）在识别、分割、检测等多种任务上都被成功地愚弄。尽管现有的研究大多集中于在分类/识别任务上愚弄深度学习，但根据调查的文献，我们可以很容易地观察到，深度学习方法通常容易受到对手攻击。

对抗性例子通常具有很好的泛化性：文献中所报道的对抗性例子的一个最常见的特性是它们在不同的神经网络之间有很好的传递。对于架构相对相似的网络来说尤其如此。在黑盒攻击中，对抗性例子的推广经常被利用。

对抗性脆弱性的原因需要更多的研究：关于深层神经网络对微妙的对抗性扰动的脆弱性背后的原因，文献中有不同的观点。通常情况下，这些观点并不完全一致。这方面显然需要进行系统的调查。

线性确实促进了脆弱性：Goodfello等人[23]首先提出，现代深层神经网络的设计迫使它们在高维空间中线性行为，也使它们容易受到对手的攻击。虽然这一概念很流行，但在文献中也遭到了一些反对。我们的调查指出，多个独立的贡献，保持神经网络的线性负责他们的脆弱性对抗性攻击。基于这一事实，我们可以说，线性确实促进了深层神经网络对对手攻击的脆弱性。然而，这似乎不是用廉价的分析扰动就成功愚弄深层神经网络的唯一原因。

反措施是可能的：尽管存在多种防御技术来对抗对抗对手的攻击，但文献中经常显示，通过设计反措施，可以再次成功地攻击被防御的模型，例如[49]。这一观察结果需要新的防御措施也提供一个对明显的反措施的鲁棒性估计。

高度活跃的研究方向： 深层神经网络对一般扰动的脆弱性的深刻暗示使得对抗性攻击及其防御的研究近年来非常活跃。在这项调查中回顾的大多数文献都是在过去两年中出现的，目前这方面的贡献源源不断。一方面，人们提出了一些技术来保护神经网络免受已知的攻击，另一方面，越来越多的强大的攻击被设计出来。最近，还组织了一次卡格尔竞赛。我们希望，这项高水平的研究活动最终会使深度学习方法足够强大，能够用于现实世界中的安全和安保关键应用。

8 CONCLUSION

本文首次全面综述了计算机视觉深度学习对抗性攻击的发展方向。尽管深度神经网络在各种各样的计算机视觉任务中具有很高的精度，但人们发现它们容易受到细微的输入扰动的影响，从而导致它们完全改变其输出。由于深度学习是当前机器学习和人工智能发展的核心，这一发现导致了许多设计对抗性攻击及其深度学习防御的最新贡献。本文回顾了这些贡献，主要集中在最有影响和最有趣的作品在文学。从回顾的文献来看，对抗性攻击显然是对实践中深入学习的真正威胁，尤其是在安全和安保关键应用中。现有文献表明，目前的深度学习不仅可以在网络空间中有效地攻击，而且可以在物理世界中有效地攻击。然而，由于这一研究方向的高度活跃性，可以希望深度学习能够在未来显示出相当强的对抗对手攻击的鲁棒性。